Projective Dynamics and Extended Position-Based Dynamics (Master Thesis)

This project, my Master Thesis (you can read it here or look over the presentation), presents a study focused on modern physics solvers Projective Dynamics to accelerate the calculation of deformations, making a comparison with the Position-Based Dynamics models and taking as reference the Implicit Backward Euler integration method. Therefore, a theoretical analysis of the different methods is carried out and implemented, paying attention to the development of formulations that depends on the scenario that is simulated. Finally, a battery of tests is presented that aim to provide an answer on the suitability of each solver in static and dynamic problems.

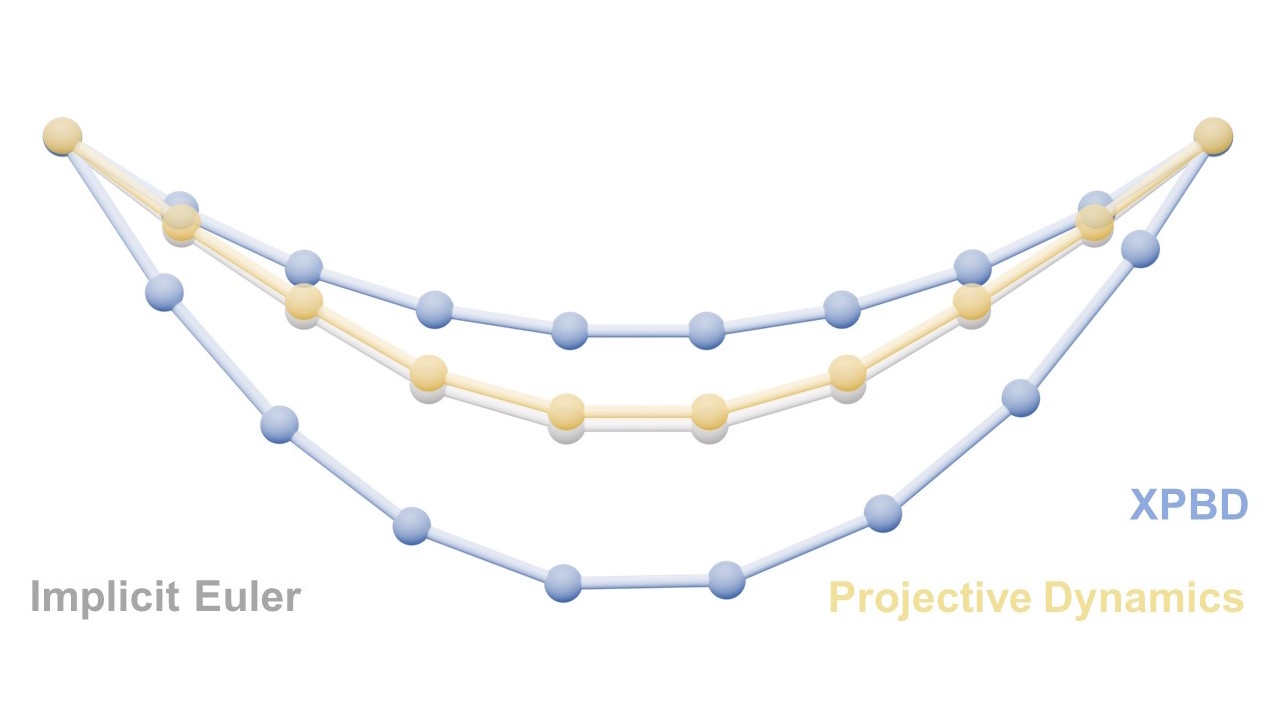
On the one hand, Extended Position-Based Dynamics (XPBD) (Macklin, 2016) was presented as an improvement to the PBD solver. XPBD is derived from a compliant constraint formulation that associates the inverse of stiffness with each constraint and introduces Lagrange multipliers, used to solve constraint oppression problems. Thus, a consistent solution is achieved that corresponds to a well-defined potential energy and with infinite iterations maintains its expected behaviour.

On the other hand, Projective Dynamics (PD) starts from the Implicit Euler integration optimization formulation. Define a local and a global step that alternates to solve the integration. Unlike Position Based, in these solvers the inertial term is considered. Among the recent PD-based methods, we chose the paper that presents this perspective for the first time, Fast Simulation of Mass-Spring Systems (Liu, 2013), and another that generalizes it to any conservative force, including general hyperelastic materials and hard constraints, ADMM - Projective Dynamics (Overby, 2017).

In summary, the project focuses on the study of these solvers in static and dynamic situations, for their viability in different large-scale simulation environments. For this, we start from a controllable scenario such as a catenary rope fixed at the extrems and different parameters are analyzed.

Some results of the study

In the following videos we see how the methods behave dynamically, comparing them with the Implicit Backward Euler reference solution (in gray).

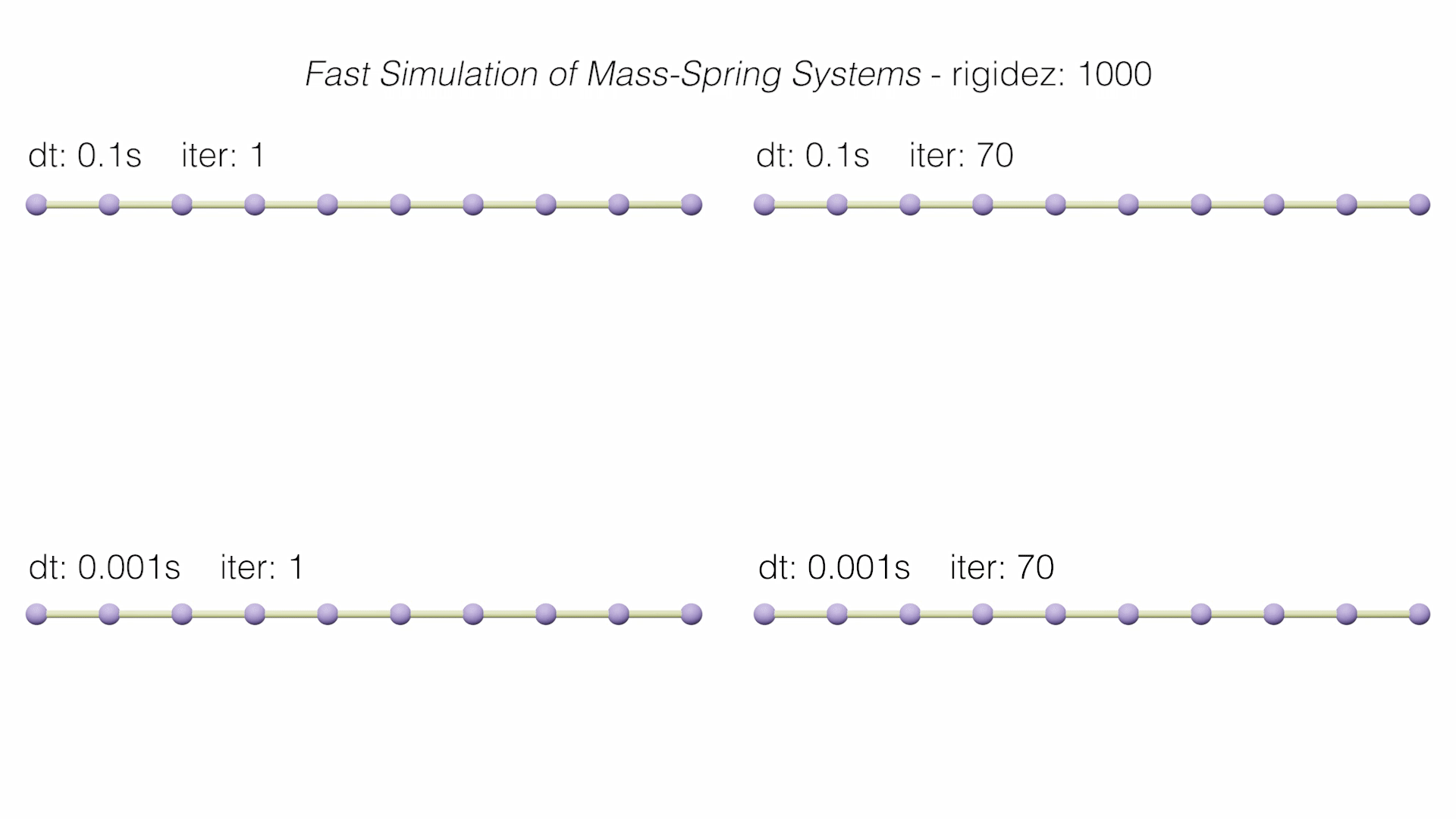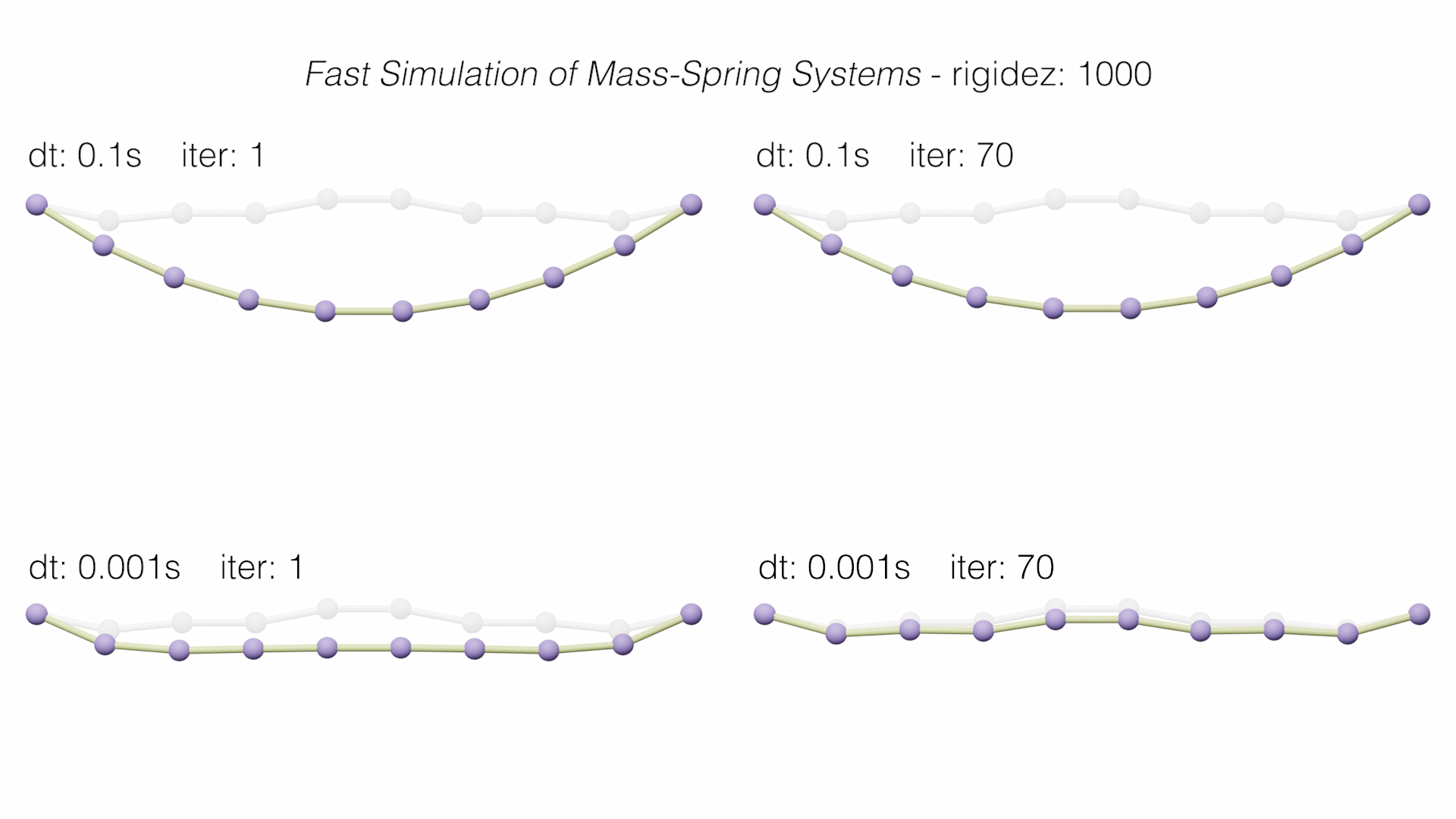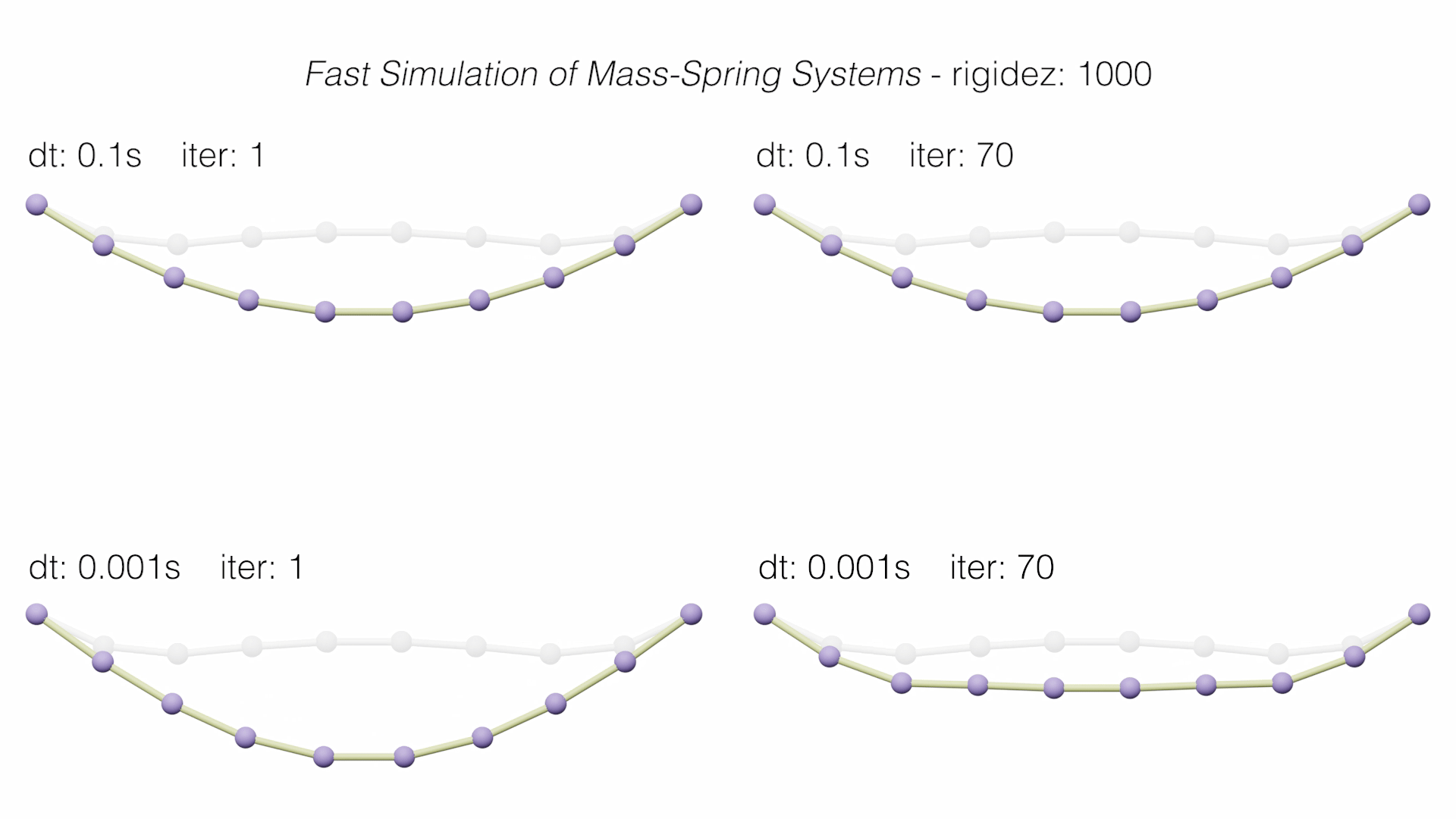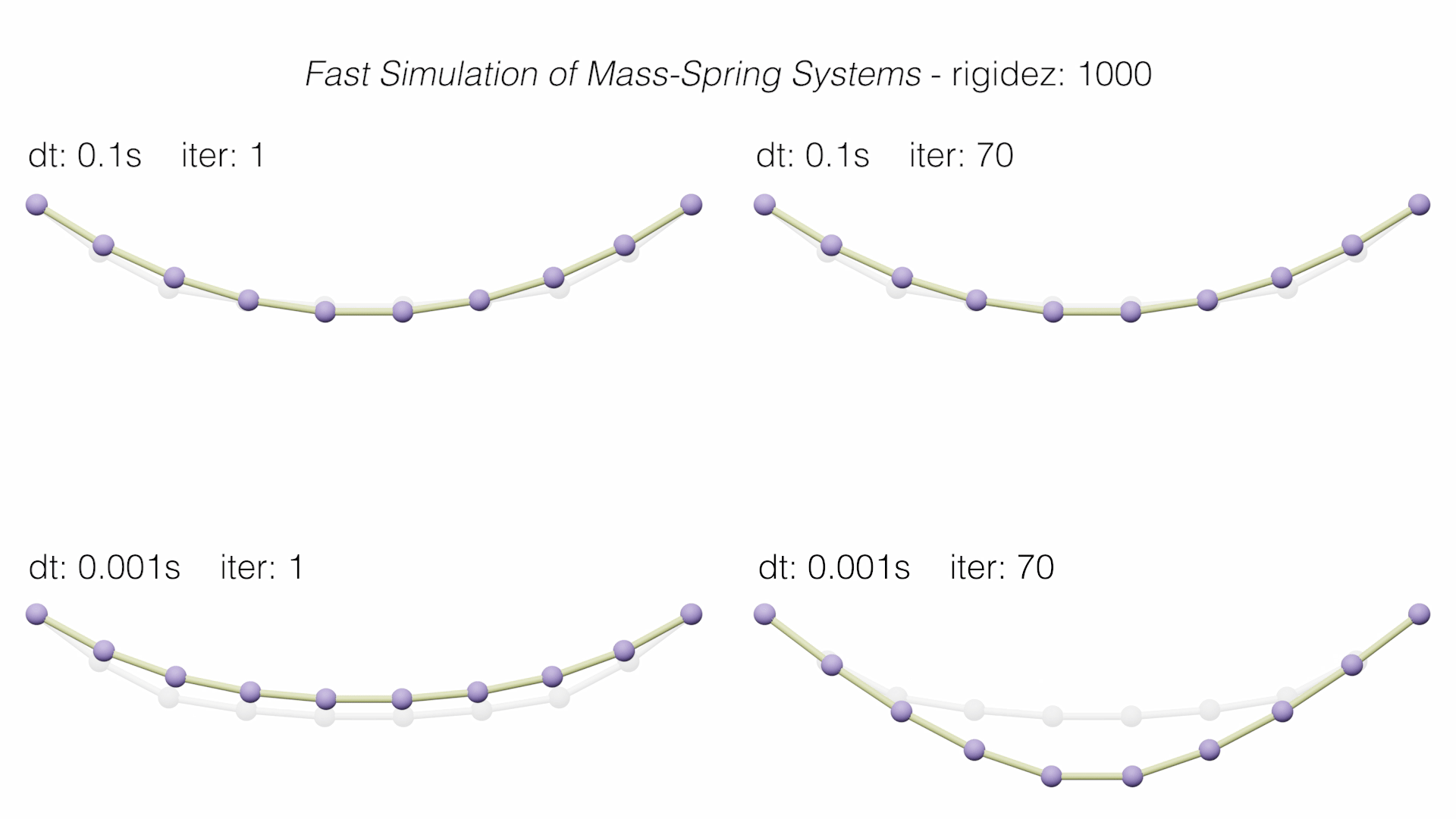
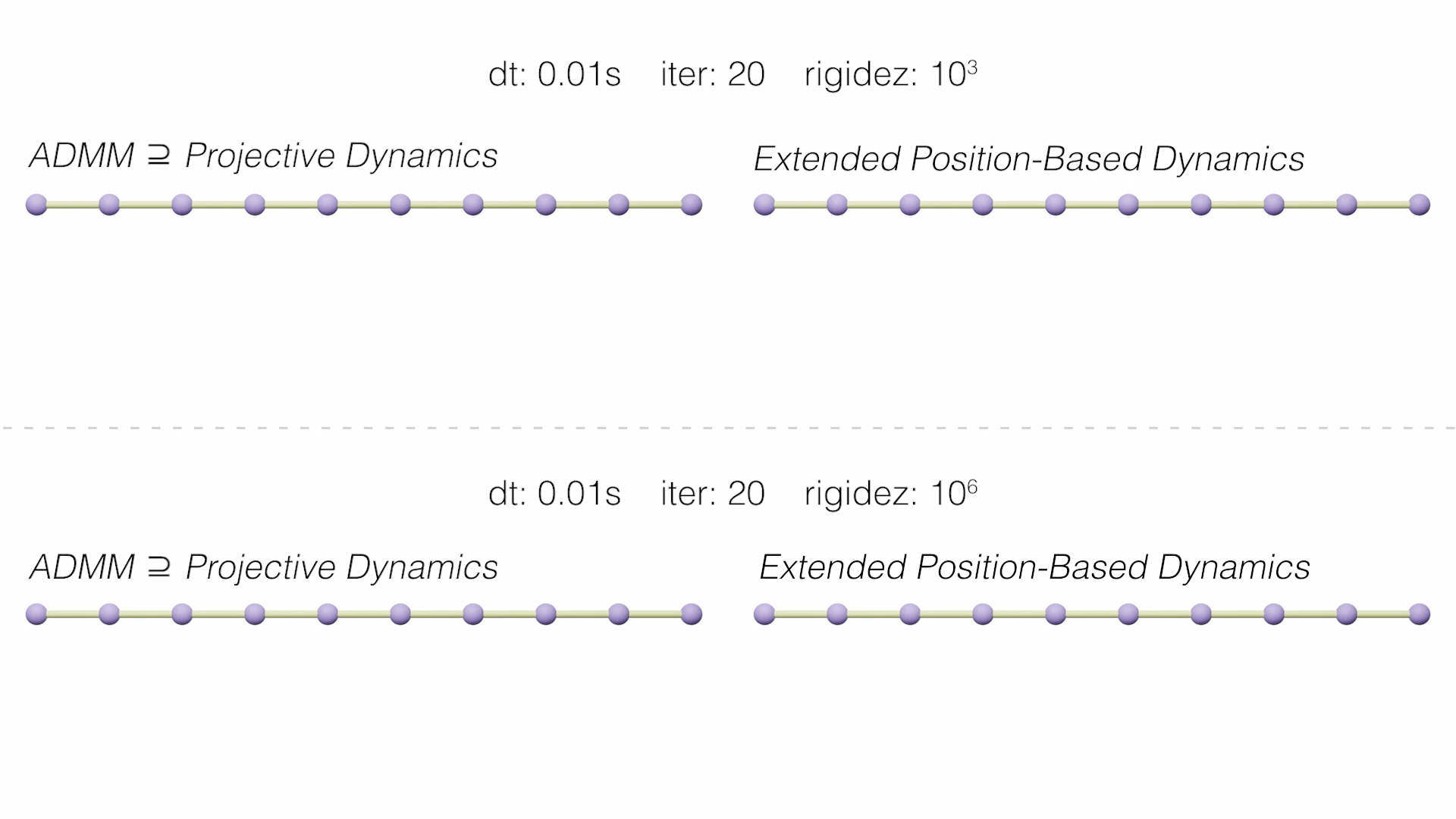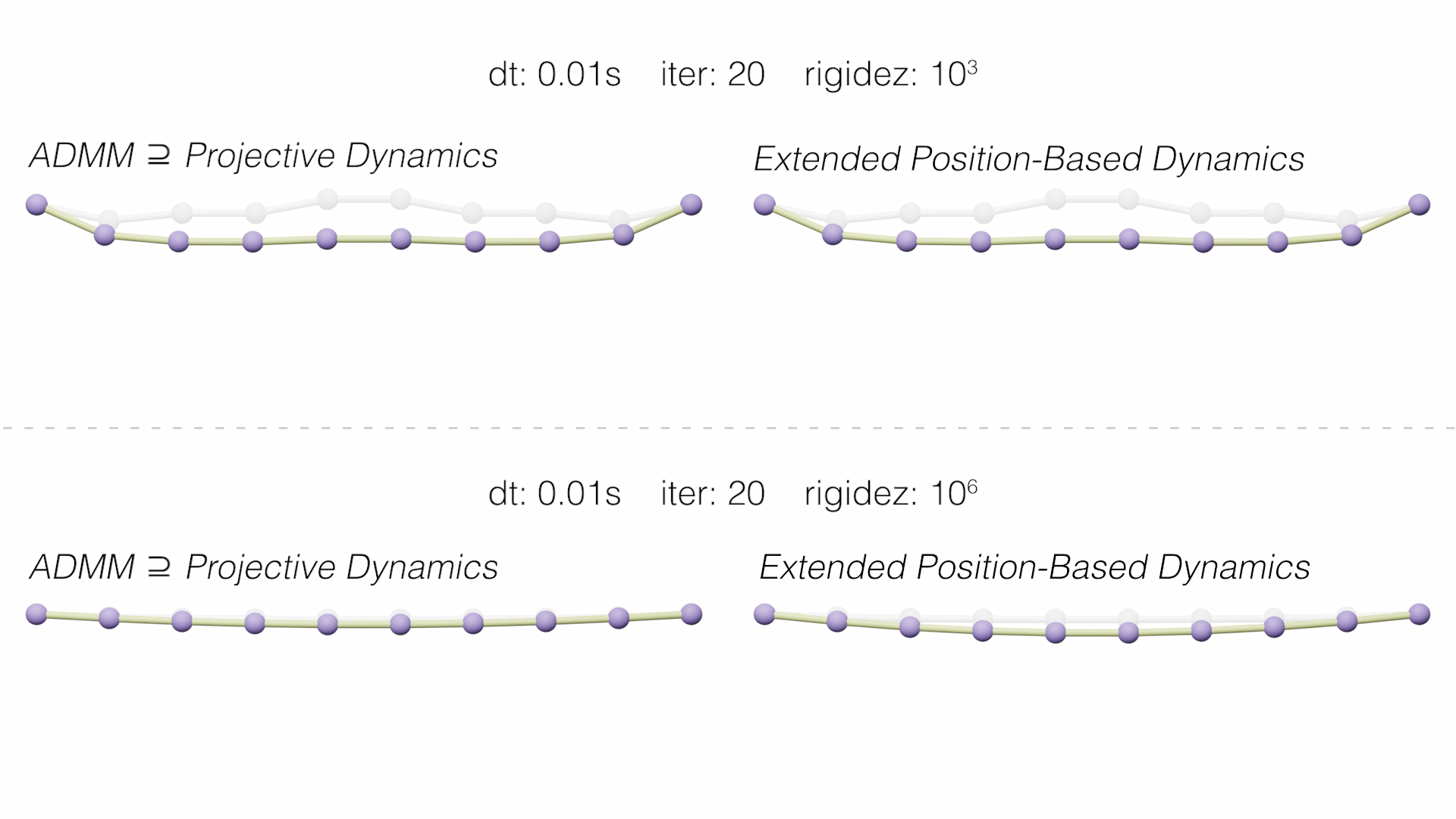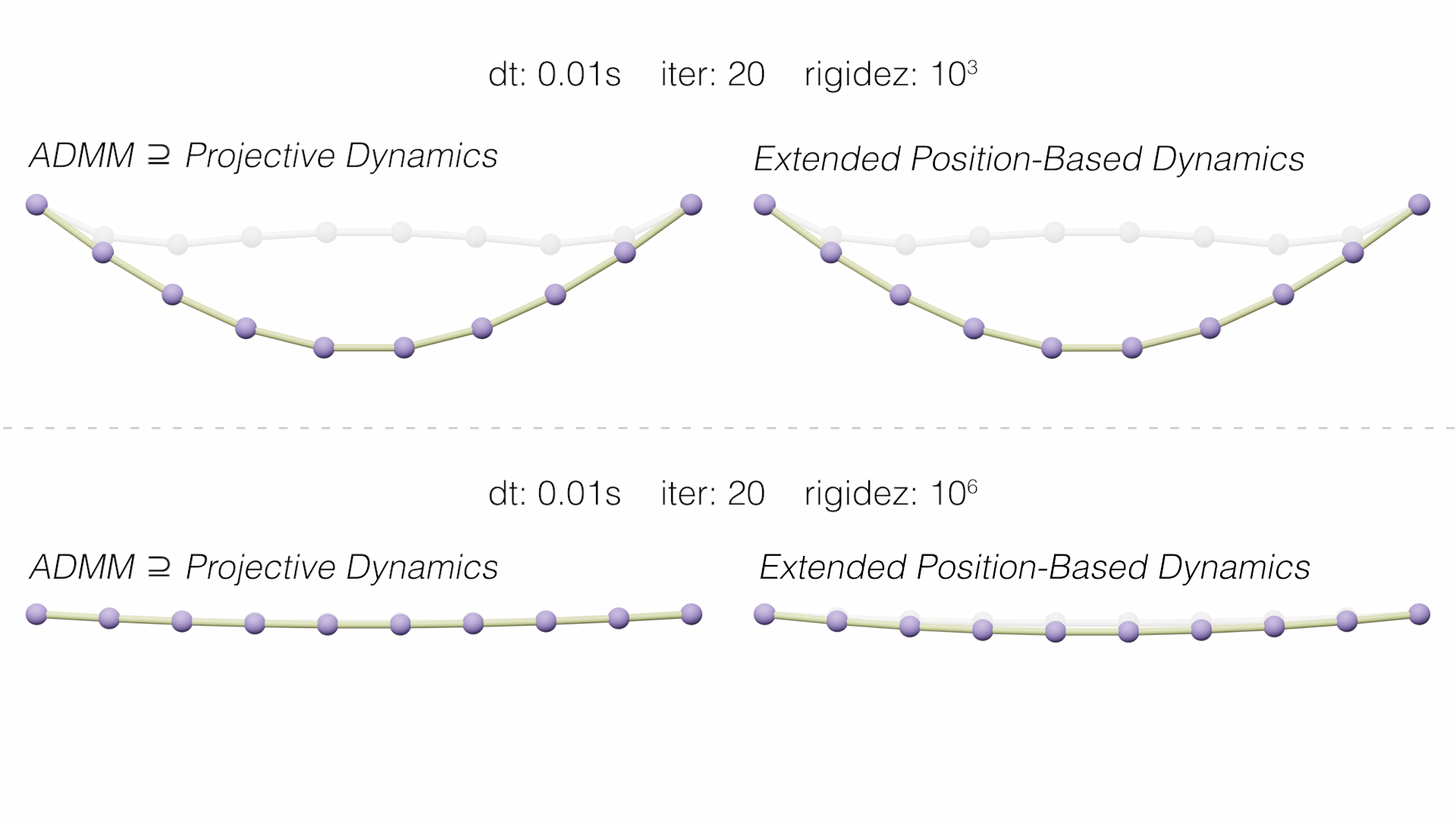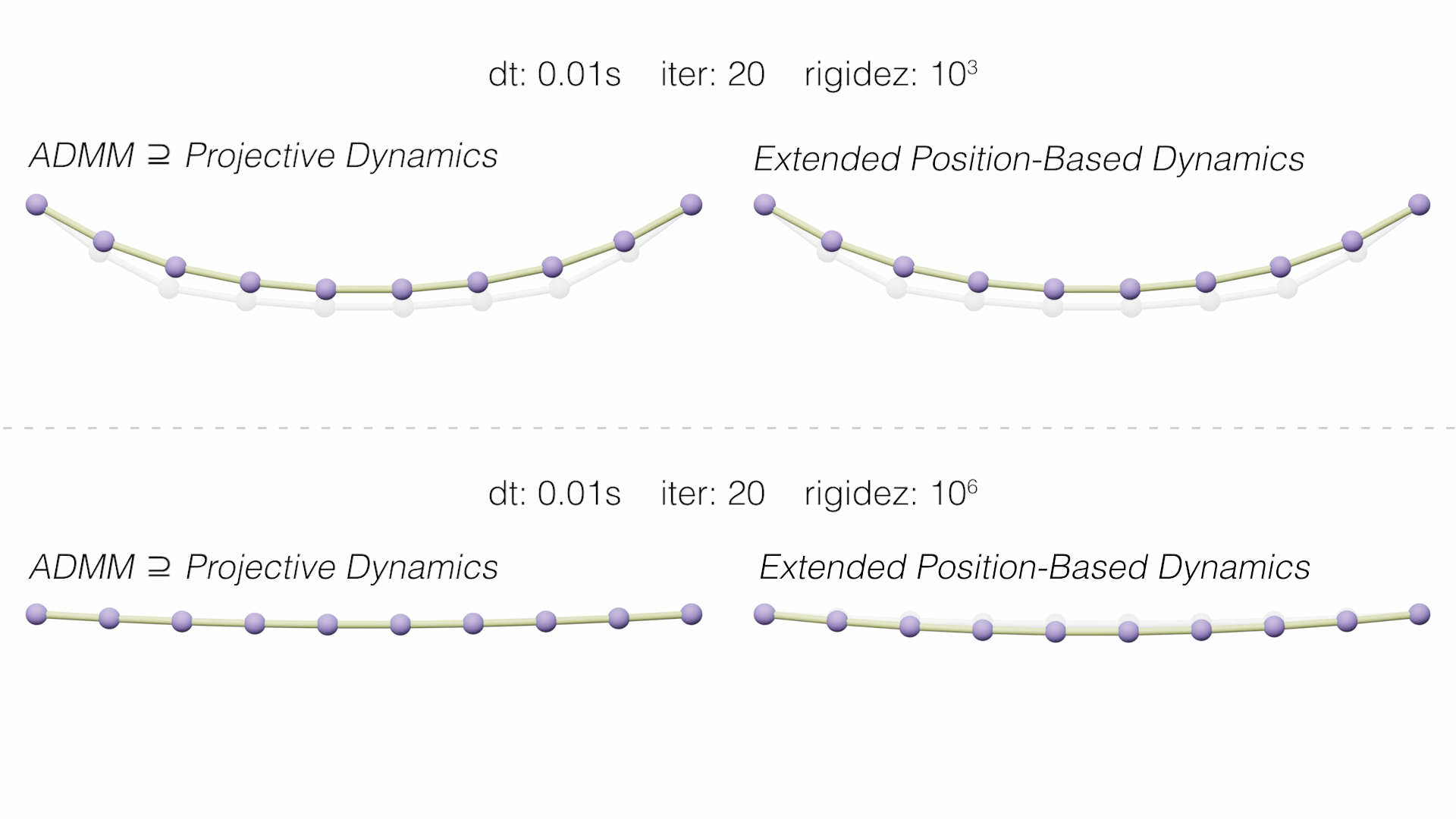
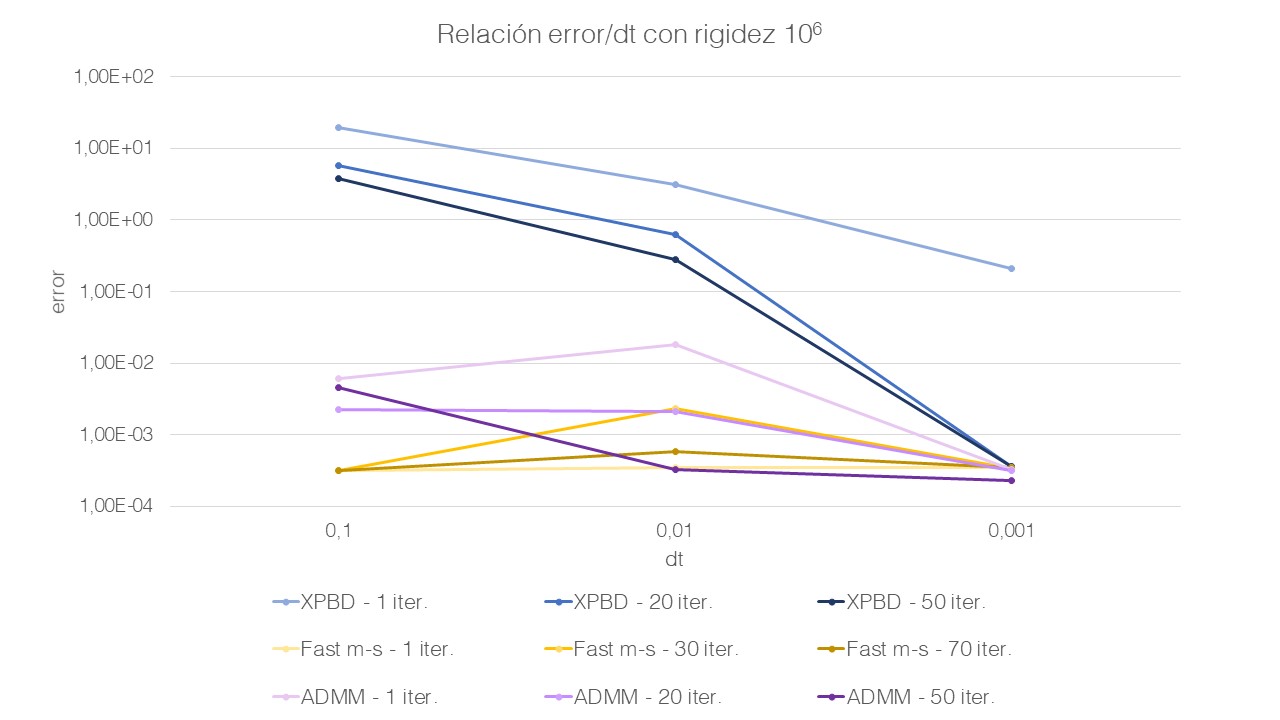
In addition, the main graph of accumulated errors in the static convergence of each method is shown.

Technical details

• 4 complex simulation algorithms have been studied and implemented (Backward Euler with Newton-Rhapson iterations as a reference).
• These methods were adapted to our scenario, refurmulating some equations and setting the boundary conditions.
• A catenary is shown in this version, but it is easily scalable thanks to the architecture of the implementation.
• Large amounts of data are handled and processed.
• Programmed in Python, C++ and MatLab. In addition, Blender have been used as auxiliary program to get the renderings.